本文旨在描述和分析集成系统中不同组件之间的关系。首先,通过机理公式或数据驱动的方法对每个组件进行建模。然后,定义各部件的边界条件,确定不同部件模型之间的参数传递方式,迭代求解各部件的参数。此外,以环境温度作为外部条件变化的例子。分析了其对各部件运行状态和系统整体效率的影响。
1. PEMFC系统模型的构建
如下图所示,本文将燃料电池系统分解为组件模型,即燃料电池堆、空气压缩机、氢气循环泵、水泵、换热器、风机、加湿器和管道。燃料电池系统的输入条件为环境温度、压力和湿度,燃料电池系统的输出为电能、热能和废气。对于氢气回路和空气回路,气体进出口的流量、温度、压力和湿度是连接各部件的边界条件。对于冷却液回路,选取流量、温度和压力作为边界条件。

PEMFC系统模型框图
燃料电池系统的参数具有强耦合性,因此需要采用数值方法对参数进行求解。该方法针对不同的燃料电池子系统,采用分治法迭代求解空气回路、氢气回路、冷却液回路、冷却空气和系统能量的耦合参数。
2. 建模
2.1 燃料电池堆模型
PEMFC的反应过程涉及到多物理场的耦合,不同类型的模型,解析的,经验的和半经验的,已经被开发用于各种目的。在这一部分中,开发了一个混合模型,以专注于关键问题并减少计算量。燃料电池的输出电压是电流密度的函数,并受燃料电池堆的温度、反应气体的流速、压力和湿度的影响。燃料电池的输出电压可表示为如下形式:
V=f(i,Tstk,qH2,qair,pH2,in, pair,in, φH2,in,φair,in)
其中,函数f 表示参数与电压得到映射。为了简单起见,这里我们使用反向传播神经网络模型从训练数据中获得反射函数。
氢气和氧气的其余化学能转化为热能。根据热能平衡,可以得到电堆冷却液的换热功率:
Qcool=Qstk-Qgas-Qlat-Qdis
其中,Qstk为电堆的热功率,Qgas和Qlat分别为尾气中的气体和水蒸气带走的热量,Qdis为散发到环境中的热量。不考虑排风的显热,因为它与其他项相比可以忽略不计。
另一个需要考虑的平衡问题是压力,即流体的流速与压降的关系,它影响着系统的工作状态和能耗。流量和压降之间的关系可以用二次多项式来近似:
△Pi=KA,iq2i,in+KB,iqi,in+KC,i
式中:K为多项式的系数,下标i表示流体类型,即氢气、空气或冷却液。
2.2 空气压缩机和氢气循环泵模型
在稳态时,由于气体的质量流量较大,与气体的热力学能量相比,空压机/氢气循环泵与环境之间的传热可以忽略不计,气体通过空压机的状态变化可以用等熵压缩过程来描述:
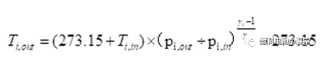
根据下面关系确定了氢气或空气的绝热指数:
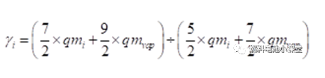
上面公式用于计算气体通过压缩机或循环泵的状态。为了评估系统的效率,还需要计算空压机或氢气循环泵的功耗。等熵压缩轴功计算公式如下:
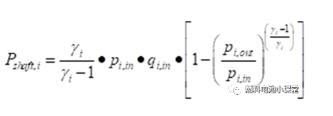
2.3 冷却系统模型
PEMFC的输出性能和寿命受到负载动态变化和系统扰动引起的温度变化的影响。因此,有效的热管理是保证高性能和长寿命的关键。根据冷却空气侧的能量平衡,冷却空气的质量流量计算如下:

为了计算冷却风扇的功耗,还必须知道空气压力。在这项研究中,假设冷却液和冷却空气的压降是流体流量的二次函数,可以通过实验来确定。与空气压缩机不同,水泵中的冷却液是不可压缩的,因此可以简化水泵耗电量的计算公式,假设耗电量是冷却液流量的二次函数。
2.4 管道模型
系统管路的设计需要考虑成本以及管路中流体压降对辅助元件功耗的影响。管道模型主要由流体力学基本方程组成[ 15 ]。流体在管道中的流动阻力可分为两种类型。一种是沿管道直线段的摩擦压降,另一种是由管道形状变化引起的局部压降。
管道摩阻压降采用达西-威斯巴哈方程估算:

其中,λ为摩擦系数,L为管道长度,D为管道水力直径,υ为管道流速,ρ为管道密度。上式中,摩擦系数可以表示为雷诺数的函数:

采用线性关系计算了雷诺数在2100 ~ 4000之间过渡区域的摩擦系数。雷诺数是根据水力直径定义的:
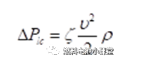
式中:局部阻力系数ζ由试验数据确定。
干空气和湿空气的压降近似为流量的二次函数,可以通过实验数据获得。选取进入和离开元件的三种流体的流量、温度、压力、湿度等参数作为边界条件。本文设计了一种迭代算法,通过计算机求解部件间的参数耦合。
3 结果和讨论
本研究以不同环境温度下的模型计算结果为例,说明了系统中各部件和电堆之间的耦合模式。环境温度值从10℃变化到30℃,每隔2℃进行一次计算;系统净输出功率从5kW变化到20kW,每隔5kW进行一次计算。下面的所有结果都是在各种工况下计算的稳态值。
3.1 电堆
下图显示了在不同环境温度和净输出功率下,由模型计算得到的燃料电池电堆的输出。当净输出功率较小时,如5 k W时,电堆输出功率大于热功率,换热器热负荷较小。即使在强制对流换热温差较小时,电堆输出功率也会保持不变。此外,由于冷却气流变化较小,冷却风扇的功耗不会显著增加。

燃料电池堆输出:(a)电流(b)电功率(c)热功率
为了提高系统的净输出功率,需要从电堆中吸取更多的电流。但是,电堆的发热功率占比随着电流( 54 A时为54.5 % , 280 A时为42.9 %)的增大而增大,导致电堆的电效率降低,维持系统运行需要消耗更大的辅助功率。因此,电堆的输出功率明显大于系统的净输出功率。当净输出为20 k W时,电堆输出功率需大于25 k W,以提供必要的辅助元件功耗。随着环境温度的升高,冷却风扇的负荷进一步增加,电堆的输出功率从24.3 k W显著提高到25.9 k W,提高了6.6 %。
从结果可以看出,系统净输出功率、电堆输出功率、电堆热功率以及辅助部件功耗之间存在耦合关系。在大功率、高环境温度条件下,这种耦合关系造成的结果差异更为明显。电堆需要输出更多的功率,以保证辅助部件在大功率下运行。冷却系统的热负荷增大,冷却气流速度对传热温差的变化更加敏感。换热温差的急剧变化提高了冷却气流速率,进而导致辅助部件的能耗增加。
3.2 部件
燃料电池的氢气消耗量和循环流量与输出电流直接相关。根据上一节对电堆的仿真结果和讨论,当净输出功率较小时,环境温度的变化对冷却风扇的功耗影响不大,电堆的输出电流几乎保持不变。在高净输出功率下,辅助组件功耗增大,电堆输出电流对环境温度的变化更加敏感。如下图 ( a )所示,总氢气流量的模拟结果与电堆的结果一致,即在低功率下,进入电堆的总氢气流量几乎不受环境温度的影响,而在高功率下,它们随环境温度显著增加。图中的氢耗量并不是简单的线性关系,而是由于其他因素(如环境温度)的影响而呈现出复杂的非线性。
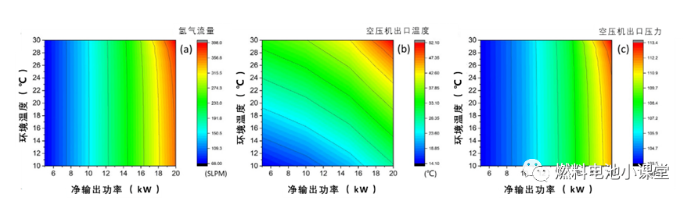
部件结果:( a )氢气流速;( b )压缩机出口温度;( c )压缩机出口压力。
燃料电池堆工作点的变化决定了对空气参数的要求,从而影响空压机的工作状态。空压机出口温度和压力影响电堆的输出性能,因此空气供给系统与电堆之间存在相关性。上图( b ) ( c )给出了空压机出口空气温度和压力的仿真结果。两个因素决定了压缩气体的温度。一种是气体等熵压缩产生的热量,另一种是空气压缩机旋转加热空气产生的摩擦热。因此,当电堆输出大功率时,气流和压力以及辅助功耗较大,空压机出口温度较高。在实验工况范围内,空压机出口温度由14.1℃升高至52.1℃,压力由103.5kPa升高至113.4kPa。
燃料电池的空气流量和化学计量比比氢气大,各功率点的压差比氢气明显,所以压缩机比氢气再循环泵对电堆输出功率和环境温度的变化更敏感。此外,由于阴极出口气体( COG )携带大量热量,空气压缩机与冷却系统之间的强耦合作用不可忽略。
冷却系统对热功率和环境温度的变化更为敏感。必须保证一定的冷却液流量才能使冷却液通道内的对流换热更加充分,同时冷却液流量还受到电堆进出口温差的限制。图4说明了冷却剂回路的冷却剂流量、阴极出口气体( COG )热量和冷却空气流量的模拟结果。冷却液流量随净输出功率增大而增大,与冷却液回路压降呈正相关,使得泵耗功随热负荷增大而增大。
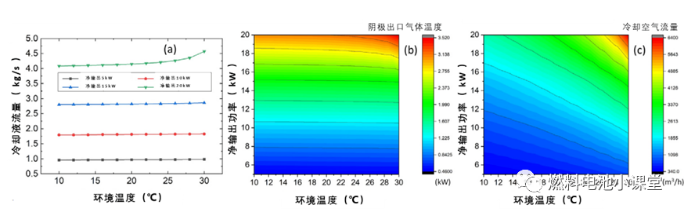
冷却液回路结果:( a )冷却液流量;( b )阴极出口气体温度;( c )冷却空气流量。
燃料电池电堆产热与散热之间的平衡是维持燃料电池电堆温度恒定的关键。阴极出口气体携带大量热量,在系统设计中不可忽略,包括气体和液态水的显热以及气态水的汽化潜热。从上图 ( b )中的结果可以看出,阴极出口气体所携带的热量随着电堆功率的增加而增加,这是由于在高功率下有更大的气流速率和更多的气态水。当净输出功率为5 k W时,排气热量只有0.46 k W,当净输出功率为20 k W时,排气热量高达2.5 k W。除阴极出口气体外,电堆产生的热量主要由冷却系统排出,在小功率时冷却气流速率对环境温度的变化不敏感。随着电堆热功率的增加,冷却气流速率急剧增加,需要更多的输出功率来弥补BOP的功耗,这与上述结果一致。
电堆的输出能量决定了热源的功率并驱动冷却系统部件工作,冷却系统决定了散热器的功率。电堆和冷却系统是相互关联和制约的。环境温度的升高会显著增加大功率下的散热负荷。在保证系统净输出的前提下,电堆的功率输出最终会增加,电堆的电效率会降低。
3.3 系统效率
从以上讨论可以得出,燃料电池系统和电堆的内部组件是相互联系、相互制约的。根据给定的净输出功率和环境温度,可以确定系统中各部件的状态。冷却风扇、水泵、氢循环泵和空气压缩机的功耗会随着环境温度的升高而增加,电堆需要输出更多的功率才能保证净输出功率,电堆效率和系统效率均有所降低,如下图所示。在低功率下,不同环境温度下BOP的功耗几乎不变,但在高功率下,环境温度对BOP功耗的影响更大,两者呈指数关系。系统电效率的变化规律与BOP功耗的变化规律相反。

图(a)BOP功耗(b)系统效率
电堆及各部件的特性、系统设计参数、系统运行工况决定了整个系统的能耗和效率。在设计系统和优化运行工况时,需要考虑各部件并分析其耦合关系,以获得系统效率的最优解。
注:
 切换行业
切换行业




 正在加载...
正在加载...




