基于非线性电化学阻抗的燃料电池故障诊断
No.1
研究概述
电化学阻抗谱(Electrochemical impedance spectroscopy, EIS)有助于燃料电池故障诊断工具开发,对提升其使用寿命具有重要意义。传统阻抗测量受限于一阶线性响应,而非线性电化学阻抗考虑额外的高阶谐波响应,可提升故障诊断的输入维度。本研究提出一种基于非线性电化学阻抗谱(Nonlinear electrochemical impedance spectroscopy, NEIS)的故障诊断方法,首先分析激励幅值对NEIS影响,然后开展不同程度的水淹、膜干和缺气故障实验;在此基础上分别建立EIS和NEIS数据集,并利用主成分分析提取主要特征;最后利用支持向量机和随机森林构建故障诊断模型,且采用混合遗传粒子群优化算法对模型的超参数进行优化。
No.2
基本定义
在传统EIS测量过程中,一般采用较小激励幅值,以减小非线性对EIS测量影响。若采用相对较大激励幅值,对输出信号进行时频转换后可观测其非线性响应结果。图1给出了燃料电池在电流激励下的电压时频响应,当受到角频率为的周期性信号激励后,输出结果是一个偏离基频的周期性信号,其傅里叶级数展开如下:

式中,下脚标k为谐波数,当k=1为基频响应信号,是燃料电池线性频响结果;当k≥2时,为高阶谐波响应结果,反映了燃料电池的非线性特征。Yk和Ψk分别为k次谐波振幅和相角偏移量。对于线性定常系统,脉冲响应h(τ)可以通过与输入u(t)的卷积来描述其输出:

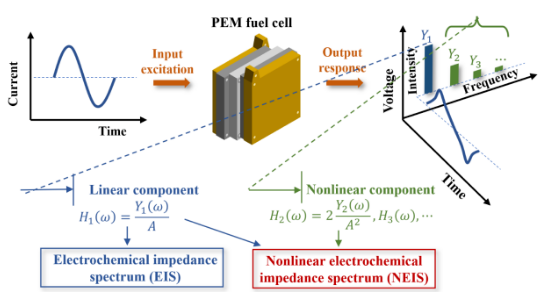
图1 燃料电池非线性电化学阻抗基本定义
No.3
实验设置
本研究对象为活性面积25 cm2的商用膜电极,Scribner 850e测试台控制反应条件,并内置了阻抗分析仪和电子负载。高精度NI数据采集卡对燃料电池电压和工作电流进行采集。待燃料电池在预设工作条件下稳定工作30分钟后,将0.1 ~ 1 kHz频率范围正弦激励施加于燃料电池,具体测试频率范围及采样周期如表1所示。

No.4
激励幅值确定
在传统电化学阻抗谱测试中,为保证燃料电池保持线性响应,激励幅度须设定较小值,如5% ~ 10%;在NEIS测试中,激励幅值对高次谐波显示度非常重要,但同时也要避免激励幅值过大导致三次及以上谐波响应不可忽略,给非线性阻抗计算带来困难。为此,在常用工作条件(空气/氢过量系数:2.0/1.5;空气/氢气湿度:50%/50%;空气/氢气压力:100/120 kPa;电池温度:75℃)下,依次对燃料电池施加幅值为工作电流5%、10%、15%、20%的正弦激励,以确定合适的激励幅值。
不同激励幅值下电化学阻抗谱、一阶频率响应函数H1(w)和二阶频率响应函数H2(w)如图2所示,从结果可看到电化学阻抗谱和H1(w)对激励幅值变化不敏感,H2(w)则对激励幅值变化敏感,尤其是在电流密度为0.6 A/cm2时,低于10%的激励幅度无法得到平滑H2(w),而当激励幅值为3%时依然可得到平滑H1(w)。但激励幅值不能选择过大,防止等式(7)和(8)无法成立,因此最终选择激励幅值为15%用于非线性阻抗计算。
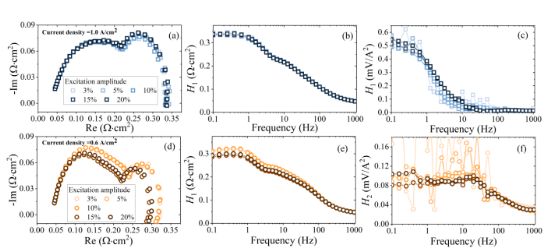
图2 不同激励幅值下Nyquist图、一阶频率响应函数H1(w) 和二阶频率响应函数H2(w) (第一行电流密度为1.0 A/cm2;第二行电流密度为0.6 A/cm2)
No.5
故障数据集及故障特征选取
根据操作条件对内部状态影响敏感性,设计如表2所示的故障条件,在此基础上开展故障实验并进行非线性阻抗测量。本故障数据集总共包含180个样本,故障标签设置同样如表2所示。不同故障条件下每个样本H1(w)和H2(w)的平均值如图3所示,可以看到一阶响应H1(w)和二阶响应H2(w)均能在特定频率段区分不同故障类型,且H1(w)和H2(w)变化趋势基本一致。本研究将仅包含H1(w)的数据集定义为传统EIS数据集X1,将包含了H1(w)和H2(w)的数据集命名为NEIS数据集X2。
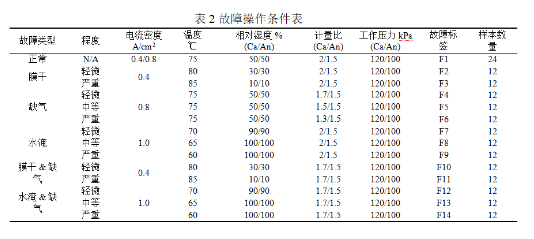
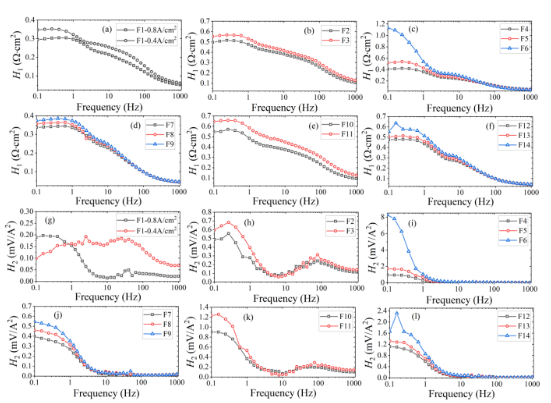
图3 不同故障标签下(a)-(f)一阶频率响应函数和(g)-(l)二阶频率响应函数
在燃料电池故障诊断模型中,故障特征构建至关重要。数据集X1和X2中变量较多,容易导致信息冗余;另一方面,样本中潜在噪声也可能影响诊断精度。对原始数据进行适当特征提取,可有效降低模型复杂度和计算成本,本研究采用主成分分析提取故障特征并进行降维,新合成变量称为主成分,可代替原有高维变量来表达系统大部分信息。对传统电化学阻抗数据集和非线性电化学阻抗数据集进行主成分分析,结果如表3所示。一般情况下,主成分累积方差贡献率达到85%以上即可显著地代表原变量主要信息,对于数据集X1,前两主成分累积方差贡献率为97.349%,因此将其作为特征变量;对于数据集X2,选取前5个主成分作为独立变量,其累积方差贡献率为94.967%。

No.6
故障诊断模型及结果
在众多经典分类模型中,支持向量机(Support vector machine, SVM)避免了从传统归纳到演绎的过程,实现了从训练样本到预测样本的高效推理,具有良好鲁棒性。此外,为了避免单一模型的随机性,还采用运行效率高、抗噪声能力强的随机森林(Random forest, RF)补充验证非线性阻抗特征的有效性。同时,采用混合遗传粒子群优化算法(Hybrid genetic particle swarm optimization, HGAPSO)对SVM和RF超参数进行优化,具体流程如图4所示。

图4 基于混合遗传粒子群优化算法的SVM和RF超参数优化
在完成故障数据集X1和X2特征提取后,随机抽取各数据集135个样本作为训练集,对诊断模型进行离线训练,其余45个样本定义为测试集用于模型精度评估。模型诊断准确率定义为正确诊断的样本与测试集中所有样本的数量之比。诊断结果如图5所示,对于EIS数据集,SVM诊断准确率可达93.3%,在水淹故障程度识别中存在两个错误样本,在水淹混合缺气识别中存在一个错误样本。在超参数优化下,HGAPSO-SVM在水淹故障程度识别中避免了一个误差样本,总体检测准确率为95.56%,但分类结果仍有待提高。同样,由于5个样本被错误诊断,RF总体准确率为88.90%,优化超参数后,虽然误诊断样本数量减少到3个,但精度仍有待提高。当利用NEIS数据集进行模型训练和测试时,SVM和RF故障诊断准确率均可达到97.78%,因此与传统EIS数据相比,NEIS可提供更多故障特征提高诊断精度,表明非线性阻抗在燃料电池故障诊断中的先进性。此外,HGAPOS-SVM可实现100%正确诊断,表明参数优化可提高模型特征提取能力。然而,HGAPSO-RF仍然无法正确识别一个轻微水淹缺气混合的故障样本,这可能与RF本身特征提取能力有关。综上所述,相比传统EIS,基于NEIS进行故障特征提取,不仅能够准确诊断出水淹、膜干、缺气及其混合故障类型,而且在故障程度上具有更好的区分能力。
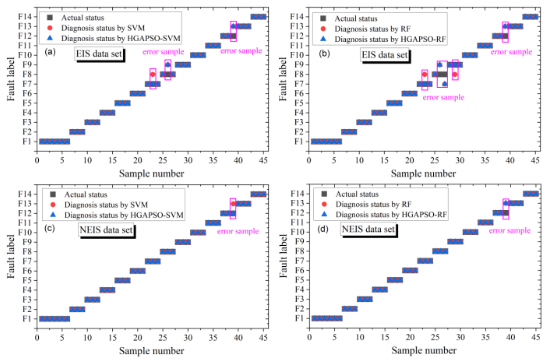
图5基于(a)(b)传统电化学阻抗EIS和(c)(d)非线性电化学阻抗NEIS的诊断结果
论文引用
Hao Yuan, Shaozhe Zhang, Xuezhe Wei, Haifeng Dai. Fault diagnosis of proton exchange membrane fuel cell based on nonlinear impedance spectrum. Automotive Innovation, 2023.
 切换行业
切换行业






 正在加载...
正在加载...




