摘要:转速轴是空压机的关键部件,用于联接涡轮盘、轴承座等零件。由于转速轴在高转速、高温度、变负荷条件下工作,工作条件恶劣,因此转速轴工作可靠与否直接影响空压机的寿命和安全。转速轴不仅传递扭矩还承受转子自身的重力、不平衡力等影响。将空压机转速轴模型分为携带涡轮和不携带涡轮两种结构分别进行自由模态分析。并将两种分析结果进行对比,为某空压机整机振动提供试验数据并进行详细分析,为后续相关研究奠定基础。
引 言
氢燃料电池汽车专用空压机是燃料电池供气系统的核心部件。转速轴是空压机的做功部件,通过旋转对气体作功,使气体获得压力能和速度能。转速轴要有足够的强度和刚度,防止运行时产生位移,造成摩擦、撞击等故障,同时应避免临界转速所产生的的共振对空压机造成损坏。Lucian Witek 等通过实验的方法深入研究了一种利用空气压缩机的叶片在激振力的作用下,使其在共振状态下受到破坏点的扩展,并通过有限元法深入研究了这种叶片在该区域的共振状态下的应力状态。Zhao Yuanyang等通过研究30 kW燃料电池系统中空压机临界转速对性能的影响,从而验证空压机应当避免在临界转速下工作,从而进一通过物理材料提升空压机工作效率。韩永杰等人对一种新型采用离心式空压机的燃料电池系统的性能情况进行了仿真和研究,与国内目前采用旋涡式空压机的燃料电池系统的性能情况进行了对比和分析。结果显示:采用离心式空压机的燃油动力电池系统在其运行时间和范围内都能够满足常用系统的运行时间范围,且该系统的工作效率也更高,空气加湿性能更好。任天明等人通过利用动力学设计,对空压机转子进一步优化设计,从而大幅提高了空压机转子的临界转速,并通过降损设计有效减小了转子搅水损耗。空压机最终达到了100 000 r/min、10kW的设计目标,实现了稳定运行。
文中通过对燃料电池空压机转速轴的两种模型分别进行自由模态分析,得出转速轴是否所携带涡轮对实验结果影响较大,并在今后的研究试验中对空压机控制策略进行相关优化,从而避免因共振引起的机械疲劳。
1.氢燃料电池专用空压机
在氢燃料电池系统中,如果电堆作为燃料电池的“心脏”,那空压机便可称之为燃料电池的“肺”。空压机在氢燃料电池系统中负责为电堆输送特定压力及洁净空气,为电堆反应提供必需的氧气,故空压机是燃料电池系统核心的零部件之一。常见的空压机类型有离心式空压机、罗茨式空压机、双螺杆式空压机等。文中主要对离心式空压机进行相关数据分析。
离心式空压机通过旋转叶轮对气体做功,在叶轮与扩压器流道内,利用离心升压和降速扩压作用,将机械能转化为气体内能。离心式空压机具有噪音小、无油、效率高、体积紧凑、等方面的综合效果,被认为是最有前途的空气机类型之一。
在离心式空压机中,高速电机转子直接驱动涡轮在蜗壳中高速旋转,并通过扩压器提升气体压力后输出。高速电机转子直接驱动叶轮旋转压缩气体。故空压机转速轴的结构稳定性及强度的可靠性在空压机系统中起至关重要的作用。
在三维软件UG中建立燃料电池专用空压机结构CAD模型,如图1所示。结构总长为408.69 mm、总宽为232.35 mm。如图2所示,空压机主要由转子轴、定子、涡轮、蜗壳、轴承等结构组成。

图1 氢燃料电池空压 图2 氢燃料电池空压机模型 剖面图
2 .空压机转速轴建模及模态分析
2.1 .建立转速轴模型
利用三维软件UG软件,建立空压机转速轴结构CAD模型,如图3所示,并将转速轴模型命名为M1。

图3 空压机转速轴模型 图4 空压机转速轴简化模型
2.2 .模型简化
空压机转速轴与空压机箱体以及固定涡轮相连接,在不影响计算结果正确性和结构动态特性的原则下,对转子系统进行模型简化,根据转速轴结构形状的特点,忽略诸如倒角、圆孔等细节,其原因是它们只对局部强度产生较小的影响,并且在划分网格中,还需要通过较多的单元来进行模拟。故对转速轴体的倒角、键槽等特征进行简化处理,有利于降低问题的复杂程度,节省计算时间。图4为简化后模型示意图。
2.3. 基于Hypermesh的转速轴模态分析
2.3.1. 模态分析理论
模态分析作为动态分析的重要基础部分,在进行固有频率的计算分析时,通常会采用有限元法来进行分析。模态分析法获得振动频率的方法通常会由两部分组成,即实验模态分析以及计算模态分析。实验法是利用实验研究及仪器进行参数收集并进行识别,来进行模态实验的方法。文中将采用有限元分析法来进行模态分析,即利用计算机来对转速轴进行模态分析。而模态分析又有自由模态分析以及约束模态分析之分,在文中将对其进行自由模态分析。
一个N自由度的线性系统,其运动微分方程可以表示为:
[M]{x″}+[c]{x′}+[K]{x}={F}(1)
式中:[M]为系统的质量;[C]为系统的阻尼;[K]为系统的刚度矩阵;{x}为系统各点的位移响应向量;{F}为激励力向量。
[M]和[K]通常为实系数对称矩阵,而[C]为非对称矩阵,因此方程(1)是一组藕合方程。当系统的自由度很大时,求解非常困难。模态分析的算法所要解决的问题就是将藕合方程变成非藕合独立方程组。对运动微分方程式(1)两边进行拉普拉斯变换可得:
(s2[M]+s[c]+[K]){X(s)}={F(s) (2)
式中:X(s)为位移响应的拉普拉斯变换;F(s)为激励力的拉普拉斯变换。
2.3.2 .建立转速轴有限元模型
将M1模型文件转为.STP格式文件,并导入到Hypermesh中。采用六面体网格单元为主要单元形态对空压机转速轴进行网格划分,同时为提高有限元模型计算准确度,将单元尺寸定为10 mm。空压机转速轴有限元模型如图5所示,转速轴划分为17 114个单元,包括4140个节点。转速轴采用40cr型材,其相关特性参数指标为:弹性模量为210 GPa,泊松比为0.3,密度为7.9 g/cm3。

图5 转速轴M1有限元模型
2.3.3. 转速轴模态分析
通过不施加载荷与约束,对转速轴的有限元模型进行自由状态下的模态分析,提取了前12阶的固有频率与振型。前6阶模态为刚体模态,可忽略,故取转速轴柔性模态前六阶数值进行分析。表1列出空压机转速轴前6阶的固有频率,其振型见图6。
表1 转速轴固有特性
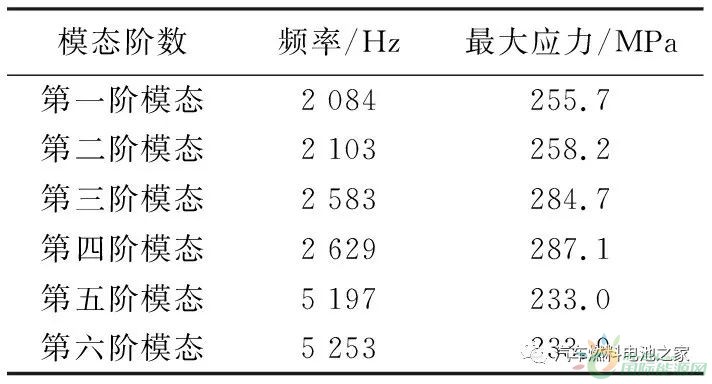

图6 转速轴1~6阶振型云图
由前6阶自由模态可见空压机转速轴频率范围为:2 000~5 300 Hz,所承受最大应力在不同频率下变化范围较小,且由振型云图可知空压机转速轴结构稳定,不会发生较大形变。
3 携带涡轮的空压机转速轴模态分析
3.1 建立携带涡轮的转速轴有限元模型
在M1模型基础上增加涡轮,建立三维CAD模型,并将其命名为M2,将其转化为.STP格式文件后导入到Hypermesh中。同样采用六面体网格单元为主要单元形态对车架进行网格划分,并将单元尺寸定为10 mm。所建立转速轴模型有限元模型如图7所示,携带涡轮的转速轴划分为31897个单元,包括9359个节点。相关特性参数指标以2.3.2材料属性进行定义。

图7 携带涡轮的转速轴有限元模型
3.2 .携带涡轮的转速轴模态分析
对携带涡轮的转速轴有限元模型进行自由状态下的模态分析。表2列出携带涡轮的空压机转速轴柔性模态前6阶的固有频率,振型见图8。
表2 携带涡轮转速轴固有特性


图8 携带涡轮的转速轴阵型图
由前6阶自由模态可见携带涡轮的空压机转速轴频率范围为:1 000~2 000 Hz,所承受最大应力在不同频率下变化范围较小,且由振型云图可知空压机转速轴最大应力均为涡轮边缘处,符合设计理论。
4 .对比分析
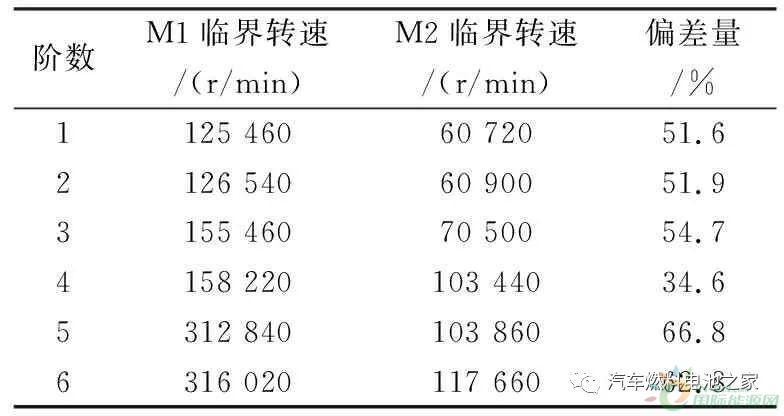
由文中2.3及3.2章节所述可知,对转速轴进行模态分析时是否携带涡轮对最终结果影响较大,如表3所列。对表1、表2数据分析,当转速轴单独进行模态分析时振动频率发生较大变化,由表3可知两种结构所得数据存在较大的偏差量。故只对转速轴进行模态分析的试验数据无实际意义。由表3中M2临界转速数据可知,该空压机转速轴在前三阶模态稳定在6~7万r/min范围之内,由于该空压机工作转速为5~8万r/min,所以在1~3阶振动模态频率会引起燃料电池系统与空压机产生共振,从而影响燃料电池系统工作效率,加大疲劳破坏,增强机械损害力度。
表3 M1与M2临界转速对比
5. 结 论
通过对某款的燃料电池专用空压机转速轴进行模态仿真分析,可以得到如下结论:
(1) 对空压机转速轴进行模态分析,转速轴是否携带涡轮对最终结果影响较大,故如果对空压机转速轴展开后续研究及优化,应将转速轴所携带涡轮与相连接轴承等其他连接部件考虑在内。
(2) 燃料电池系统的主要激励源为空压机,该空压机工作转速为5~8万r/min,由表3可知,空压机工作转速在一阶至三阶范围内,存在共振现象。故应对空压机控制策略进行相关优化,避免空压机在此转速下长时间运行。
此次研究可以有效地解决空压机共振问题,同时为今后该领域的相关研究提出重要的指导意义。
 切换行业
切换行业







 正在加载...
正在加载...




